On the equations of Poizat and Liénard
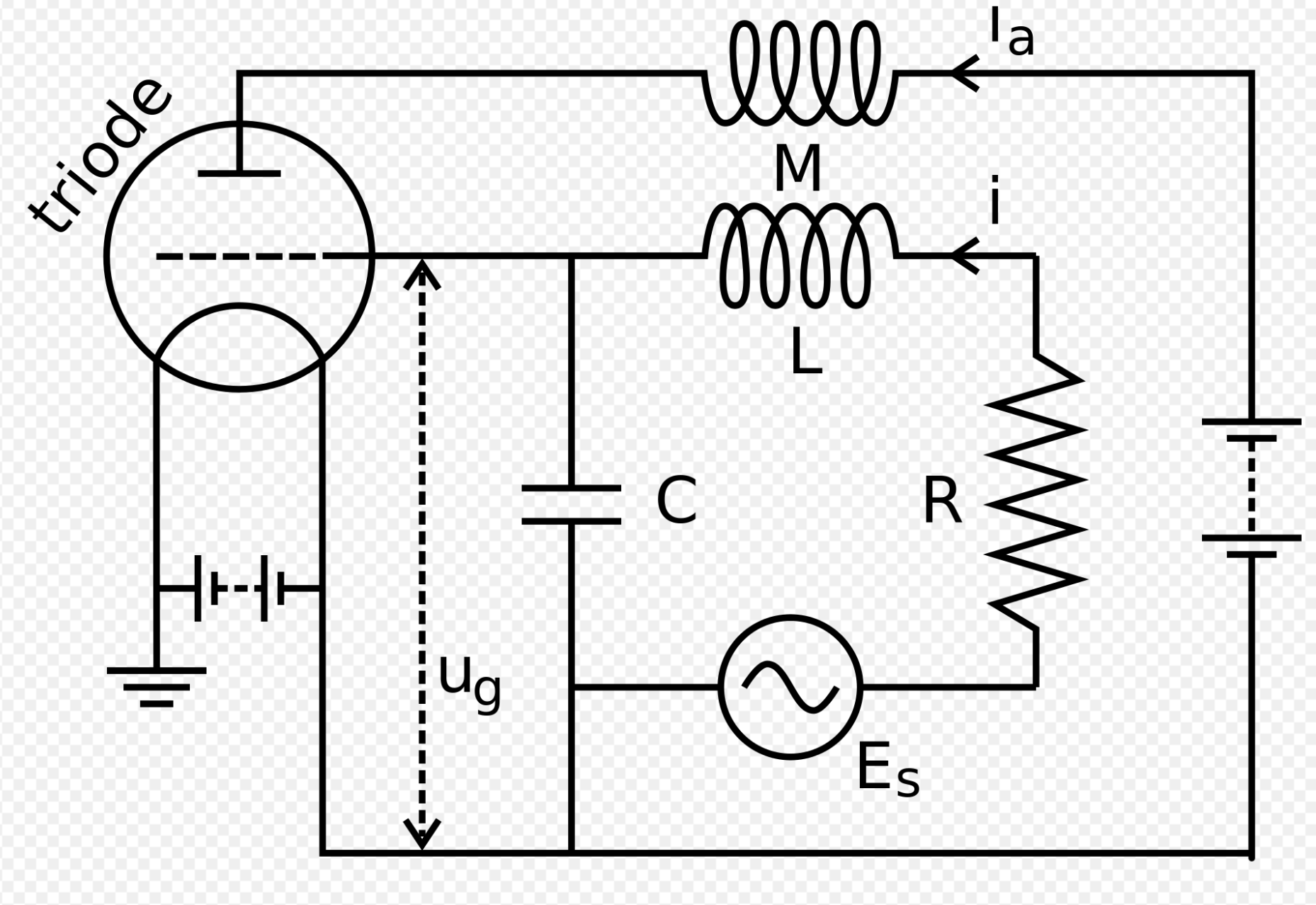
Abstract: We study the structure of the solution sets in universal differential fields of certain differential equations of order two, the Poizat equations, which are particular cases of Liénard equations. We give a necessary and sufficient condition for strong minimality for equations in this class and a complete classification of the algebraic relations for solutions of strongly minimal Poizat equations. We also give an analysis of the non strongly minimal cases as well as applications concerning the Liouvillian and Pfaffian solutions of some Liénard equations.