Rational factors, invariant foliations and algebraic disintegration of compact mixing Anosov flows of dimension 3
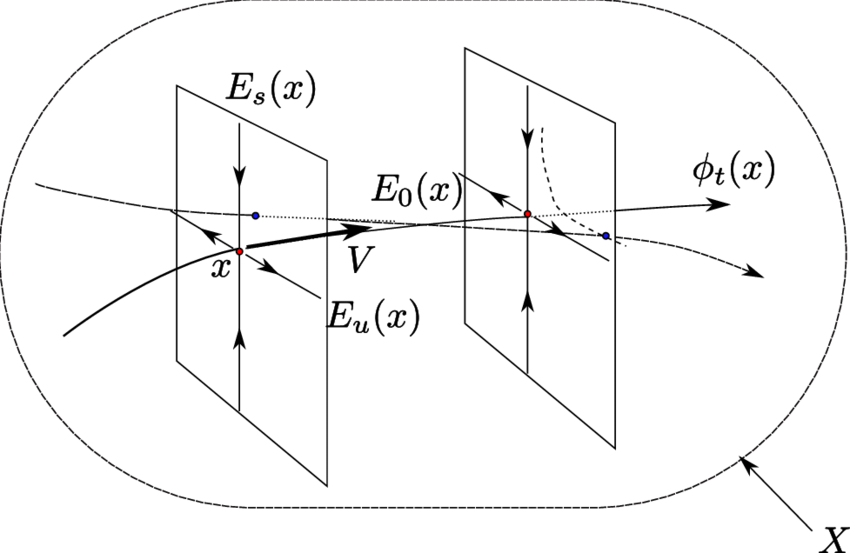
Abstract: In this article, we develop a geometric framework to study the notion of semi-minimality for the generic type of a smooth autonomous differential equation \( (X,v) \) , based on the study of rational factors of \( (X,v) \) and of algebraic foliations on \( X \) , invariant under the Lie-derivative of the vector field \( v \).
We then illustrate the effectiveness of these methods by showing that certain autonomous algebraic differential equation of order three defined over the field of real numbers — more precisely, those associated to mixing, compact, Anosov flows of dimension three — are generically disintegrated.